Andy
P
34
Stockholm
Hjälte
7 344 inlägg
2008-06-25 22:33
Godkväll alla matematiknördar!
Jag har inte orkat läsa igenom hela tråden för jag förstår ändå ingenting av det pga att jag är ett "retard" i matematikens underbara värld.
Men en arbetskamrat till mig som tydligen ska vara hyfsat hajj på matte gav mig ett problem igår som jag förstås inte förstår alls, och tänkte snabbt som attans på er! Nu vet inte jag om detta problem är svårt eller ej men han hade tydligen fått det av sin lärare i kursen matte diskret eller liknande (den kursen som är efter matematik F)
Problemet lyder:
det det är 12 väldigt fulla sjömän på en båt ute på havet, när dom berusade som dom är ska gå och lägga sig i sina sängar ombord båten, hur stor är chansen att Alla sjömän av mistag lägger sig i fel säng?
Om ni kan den så får ni gärna förklara som om du skulle förklara vad 4+4 är för ett spädbarn, Tack!
I'm back, with blazing arrows










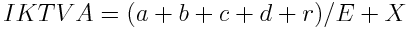
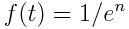 , och nu ska det visas för
, och nu ska det visas för 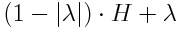 , vilket ger
, vilket ger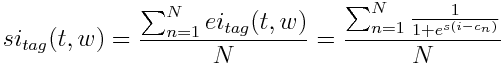
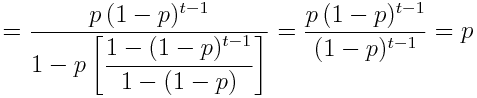
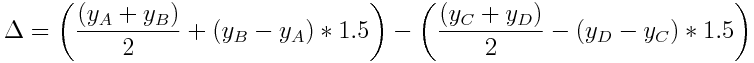
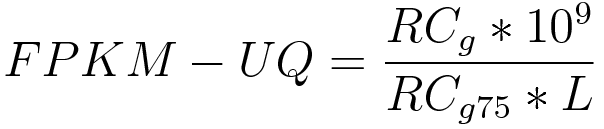 ger vänsterledet:
ger vänsterledet: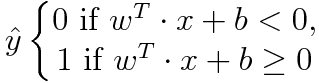
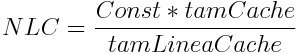 ger till slut:
ger till slut: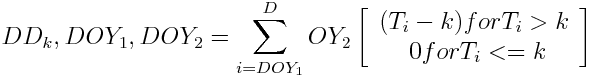
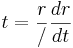 omskrivna cirkeln för vilken gäller (i) BD = CD, (ii) D och A ligger på motsatta sidor om linjen BC. Visa att, om
omskrivna cirkeln för vilken gäller (i) BD = CD, (ii) D och A ligger på motsatta sidor om linjen BC. Visa att, om 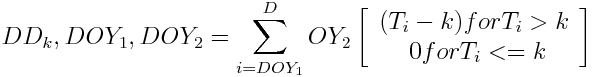 , följande gäller:
, följande gäller:
